zine folding

I recently went to a zine making workshop, where we were taught three zine folds, and shown different things a zine could be. I was very interested in the patterns of zine folding. The patterns we learned in the workshop were lacking; they were either too short or too flimsy. I wanted a zine fold pattern with plenty of pages and plenty of structure.

Over the coming weeks, I worked to develop more zine folding patterns and theories behind what made them work. This page outlines the patterns and the theories behind them.

A sturdy 16 page zine

What is a Loop Zine?

A loop zine is any zine where, when viewing the layout as you would print it, the pages make a loop.

There are fewer possible loop zines than you might think, and all possible loop zines have certain things in common. All have a number of pages divisible by 4, they form an asterisk shape when folded, they have spines between the back and front cover, and they use the entirety of one side of the sheet of paper they're made from. This style of zine requires no staples, and cleanly unfolds for easy copying.

Rules

Any possible pattern for a loop zine must follow these three essential rules:

1. The path of the zine must cross a center fold line every other fold crossing
2. The rectangle containing the zine pattern must have center fold lines that run vertically between columns 1 and 2, 3 and 4, 5 and 6, etc
3. The pages must form a closed loop

I'm pretty sure that those are the bare minimum fundamental rules that a pattern needs to follow to be a possible loop zine. Designing within those restrictions can be a bit tricky, but luckily, if we take a closer look at how those rules interact, we arrive at a very simple way to build valid zine patterns.

Rules 1 and 2 Explained

I'm a visual learner, so here are some visuals to help explain what the hell I'm talking about with those rules.

These are loop zines, so let's start with the simplest pattern: a loop of paper. Imagine this loop of paper is divided up into 16 sections.

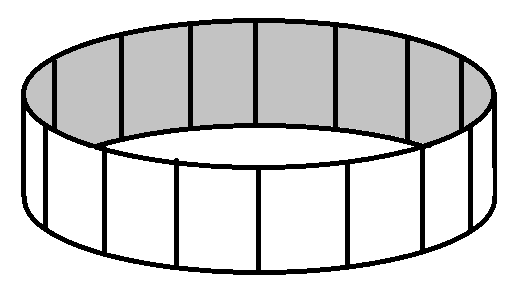
A center fold is the valley fold between a pair of pages that lies along the spine of the zine. In the case of this 16 panel loop, when when we fold it into a star, the center folds are all of the folds that are in the center of that star.

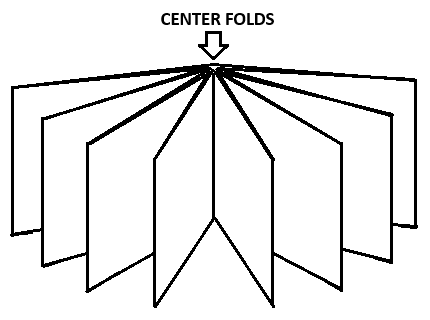
You can see in the above images that every other fold in the pattern is a center fold. In the case of this loop, the pattern goes "center, outside, center, outside, center, outside..."

That every other fold along the loop is a center fold is a rule that applies to any loop zine. Take the 16 page "-I-" zine pattern for example. If you follow the path that the pages make, every other fold along that path is a center fold, as required by rule 1. Notice also that these center folds are all collinear, lying between columns 1 and 2 and between columns 3 and 4, just like in rule 2.

You can better understand rule 1 by looking at the pages of a folded zine. If every other fold is a center fold, the off-folds should have a name too. I'm going to call them connecting folds.

A folds connect one page to the next on the top edge, V folds are connect pages at the bottom, and I folds connect on the outside edge. I folds happen when the connecting fold lies along a straight section in the sequence of pages, and A and V folds happen when the path turns.

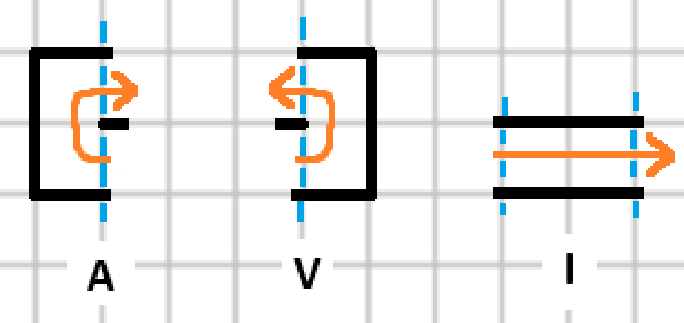
You can think of these three segments as the fundamental building blocks of a zine pattern. Every valid loop zine pattern is made up of these segments in various combinations, and any zine made with these segments will be valid, so long as it sticks to rule 3.

If you think of the zine in terms of center folds and connecting folds, there's no real difference between any valid zine with n pages except for what connecting folds link those pages together. They'll both fold up into an n page zine, but they'll just have different numbers of A, V, and I folds.

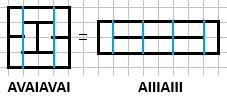
The above figure shows the fold sequence of two zine patterns. If listed in order, you can simplify a pattern down to a string of letters, much like a DNA sequence. When creating a sequence like this, it's important to be consistent about which fold is which. As the inventor of this concept, I decree that A folds are clockwise U-turns, and V folds are counterclockwise U-turns. Note that due to the looping nature of these zines, these sequences can start and end anywhere and still result in the same pattern. AVAIAVAI = VAIAVAIA

Validation by Sequence

If every loop zine pattern has a fold sequence, could we use the sequence itself to verify the validity of the pattern?

I am not a mathematician. I tried messing around with a couple ideas, but I wasn't able to come up with any validation technique better than just drawing the pattern out from the sequence, which is easy enough for a person to do. It would probably be easy to get a computer do that as well, but I can't imagine that the best way to analyze these is by drawing them out. I need to find someone who's studied graph theory.

A short list of practical zine pattern sequences

All unlabelled folds are mountain folds.

Expanding Patterns